文章来源:原理
1960年,数学家Paul Erdős和Richard Rado提出了向日葵猜想,它与大量集合的对象(例如大量散射在平面上的点),出现类似于向日葵图案的模式的频率有关。
这个问题困扰了数学家近60年之久,最近迎来了新的进展。虽然新的突破并没有完全解决这一猜想,但它却为从数学上理解复杂结构是如何从随机性中出现的提供了新的见解。
向日葵猜想与集合有关。以平面x-y上的点的集合为例,首先需要确定的是在每个集合中包含的点的固定数量,然后开始随机画环,让每个环,或者说每个集合都含有这一数量的点。环与环可以重叠,所以有的点可能会属于不止一个集合中,就像维恩图中的交点那样。
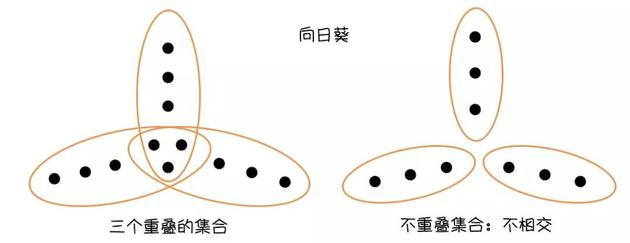
当绘制了许多包含大量点的环时,大多数环会重叠并纠缠在一起,就像一团乱麻一样。但Erdős和Rado预言,在这样的情况下,有一个微妙的结构将总是会出现:三个或更多的集合会在完全相同的点的子集上重叠,而且它们之中没有一个会与其他的任何集合重叠。
如果将这些共有的点的子集删除,那么这三个集合就会围绕着一个空隙排列,彼此之间完全分离,就像向日葵的花瓣围绕着中心黑暗的部分一样。为了解决这个问题,最简单的向日葵被认为是一种有三个彼此不重叠,也不与其他任何集合重叠的集合,这些孤立的岛屿被称为“不相交”集。
Erdős和Rado提出的猜想是,当绘制出越来越多的环时,向日葵会不可避免地出现,要么作为不相交集出现,要么作为集合以正确的方式重叠的形式出现。他们的向日葵猜想是一个更广的数学领域——拉姆齐理论——的一部分,拉姆齐理论研究的是随着随机系统变得越来越大,秩序是如何开始出现的。
Erdős和Rado想知道需要多少个点数量为多少的集合才能保证能出现一个向日葵。他们通过确立一个代表每个集合中点的数量的参数w,朝着解决这个问题迈出了一小步。然后他们证明了对于大小为w的点数集合来说,若要确保能找到一个由3个集合组成的向日葵,需要wʷ个集合。比如说,如果每个集合包含100个点,那么他们证明的是需要100¹⁰⁰个集合才能确保出现一个向日葵。
但与此同时,Erdős和Rado猜想,确保出现一个向日葵出现所需的实际集合数量应该比wʷ小得多,它更可能是一个常数的w次方,比如3ʷ、80ʷ,或5000000ʷ。然而他们却找不到一种能证明这种直觉的方法。他们懊恼于对这样一个看起来如此简单的问题,却无法取得任何进展。
自Erdős和Rado作出第一个证明至今已经过去60年,在这期间,只有两个数学家做出过进展,一个出现在1997年,另一个就是在今年早些时候由数学家Junichiro Fukuyama作出的。但他们似乎都没有能够明显改善Erdős和Rado的证明。
相比之下,最新的证明是一个突破性的进展,是由数学家和计算机科学家组成的四人小组作出的。他们将向日葵问题分解成了两种不同的场景。在第一个较简单的场景中,他们考虑的是当集合存在大量重叠时会发生什么,在这种场景下理解向日葵的出现会相对容易一些。
研究人员首先要确定的是,在这个系统中,是否存在一组在很大一部分集合中是共有的点。一旦确定了这样一组点,他们就可以把对向日葵的搜索限制在包含这组点的那部分集合中。以这种方式不断精进搜索的范围,使其包含的是系统中越来越小的一部分集合,这些集合有越来越多的共有的点。这种“修剪”将一直持续,直到他们找到向日葵为止。
第二种是更困难的一种场景,他们要分析的是当集合没有太多重叠时会发生什么。在这种情况下,最有可能产生向日葵的方法是使用三个不相交的集合。但是,要证明三个完全独立的集合隐藏在大量轻度重叠的集合中是件很不容易的事。
这就是计算机科学派上用场的时候了。几年来,论文的两位合著者Shachar Lovett和Jiapeng Zhang用来分析向日葵问题的工具与计算机科学家用来研究一种名为布尔函数的程序是一样的。布尔函数在一系列数位(0和1)上进行操作,最后输出一个单一的1(对应真)或者0(对应假)。例如,如果输入位中至少有一个是1,那么布尔函数可能会输出1;如果输入位中一个1都没有,那么则会输出0。
三年前,Lovett和Zhang意识到,使用同样的方法,也能思考在一组轻微重叠的集合中是否存在三个不相交的集合。首先要做的就是为特定集合中的每个点分配一个标签:如果它只包含在一个集合中,则为1;如果不是的话则为0。如果每个输入点都是1,那么布尔函数将输出1 (真)——意味着集合中的每个点都只在那个集合中,即集合不相交。因此,一个为“真”的结果表明具备了找到向日葵的正确条件。
研究人员严格地证明了这种对应关系,将布尔函数的知识运用到了向日葵问题上。他们证明(log w)ʷ个集合就足以产生向日葵。虽然他们的新结果并没能完全证明猜想中涉及到的集合数(某个常数的w次幂)就足以保证出现向日葵的问题。但与Erdős和Rado的wʷ结果相比,新的结果已经改善了一个数量级。
在经历了半个世纪的失败后,这项新的研究表明,一个完整的解决方案已经在望。它还进一步解释了特殊形状在随机数学领域扎根的必然性。